Mathematics Lab Activity-1 Class XI

Mathematics Laboratory Activities for class XI students Non-Medical. These activities are strictly according to the CBSE syllabus and provide insight knowledge for the students

Chapter - 1 | Set Theory
Activity 1

Objective

To find the number of subsets of a given set and verify that if a set has n number of elements, then the total number of subsets is 2ⁿ

Material Required

  Paper , Different colored pencils                                                                                

Theory

Set : A set is a well defined collection of objects.

There are two methods of representing a set

i) Roster or tabular form:

In this form all elements of a set are listed and are separated by commas and are then enclosed within braces { }. For example:  Set of all vowels in the English alphabet is

V =  {a, e, I, o, u}.

ii) Set-builder form

In this form, all the elements of a set possess a single common property, which is not possessed by any element outside the set. For example: set of all vowels in English alphabet is written as:  V = {x : x is a vowel in the English alphabet}

Empty Set: A set which does not contain any element is called an empty set or the null set or the void set. It is denoted by the symbol ф or { }.

Subset: A set A is said to be the subset of a set B, if ery element of A is also an element of B.

Procedure

1.     Take the empty set A₀ (say) which has no element as shown in fig 1.1. Subsets of A₀  is ф . So the number of subsets of A₀ is 1 = 2⁰   

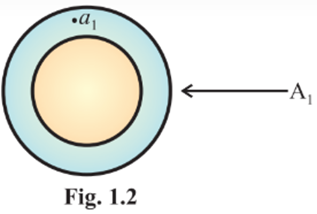
2.     Take a set A₁ (say) which has one element as shown in figure 1.2. Subsets of A₁ are ф, {a₁}. Number of subsets of A₁ is 2 = 2¹

3.     Take a set A₂ (say) which has two elements as shown in figure 1.3. Subsets of A₂ are ф, {a₁}, {a₂}, {a₁, a₂}. Number of subsets of A₁ is 4 = 2²

Fig: 1.3

4.     Take a set A₃ (say) which has three elements as shown in figure 1.4. Subsets of A₃ are ф, {a₁},{a₂}, {a₃}, {a₁, a₂}, {a₁, a₃}, {a₂, a₃}, {a₁, a₂, a₃} Number of subsets of A₃ is 8 = 2³

Observations

1) The number of subsets of A₀ is = 1 = 2⁰

2) The number of subsets of A₁ is  = 2 = 2¹

2) The number of subsets of A₂ is  = 4 = 2²

3) The number of subsets of A₃ is = 8 = 2³

4) The number of subsets of A₄ is  = 16 = 2⁴  

5) The number of subsets of A₅ is = 32 = 2⁵  

6) The number of subsets of A₆ is = 64 = 2⁶  

………………………………………………………………………………..

………………………………………………………………………………..

n) The number of subsets of A_n is   = 2ⁿ  

Result

Number of subsets of a set is given by  2ⁿ. Where n is the number of elements of a given set.

Applications: 

This activity is used to find the number of subsets of a given set.

VIVA – VOICE

Q. 1. Who developed the theory of sets?

Ans.  German Mathematician, Georg Cantor.

Q. 2. What is the utility of sets?

Ans.  Sets are used to define the concepts of relations and functions.

Q . 3. What are finite and infinite sets?

Ans. A set which is either empty or consists of finite number of elements is called a finite set otherwise it is called an infinite set.

Q. 4. What do you mean by elements of a set?

Ans. The objects used to form a set are called its elements or its members.

Q. 5. What are equal sets?

Ans. Two sets A and B are said to be equal sets if they have exactly the same elements and we write them as  A = B.

Q. 6. What is a power set?

Ans. The collection of all subsets of a set A is called the power set of A. It is denoted by P(A)

Q. 7. What is a universal set?

Ans. A set containing all elements from which the other subsets are formed is called a universal set.

THANKS FOR YOUR VISIT
PLEASE COMMENT BELOW