Mathematics Lab Activity-15 Class XI

Mathematics Laboratory Activities on Straight Lines for class XI students Non-Medical. These activities are according to the CBSE syllabus

Chapter - 9 Straight Lines
Activity - 15

Objective

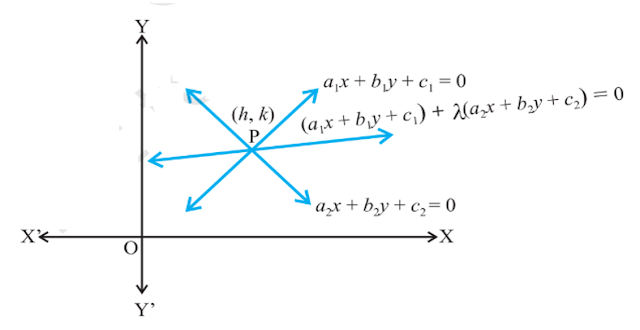
To verify that the equation of a line passing through the point of intersection of two lines a₁x + b₁y + c₁ = 0  and a₂x + b₂y + c₂ = 0  is of the form  a₁x + b₁y + c₁ = 0 + λ( a₂x + b₂y + c₂ = 0)

Material Required

Cardboard, White paper, pencil , adhesive.

Theory

Any equation of form ax + by + c = 0, where a and b are not zero simultaneously is called general linear equation or general equation of the line.

The equation of a straight line passing through the point of intersection of the two straight lines, a₁x + b₁y + c₁ = 0  and a₂x + b₂y + c₂ = 0  is of the form  a₁x + b₁y + c₁ = 0 + λ( a₂x + b₂y + c₂ = 0)

Procedure

1.Take a card board of convenient size and Paste a white paper on it .

2. Draw two mutually perpendicular lines X’OX and Y’OY to represent x-axis and y- axis respectively.

3.Take a suitable but same scale for marking points on x and y-axis

4. Draw the graph of two intersecting lines and mark their point of intersection as (h, k) as shown in fig. 15.1

Figure 15.1

5. Let the equations of the two lines be:-

3x - 2y = 5 or 3x - 2y – 5 = 0
3x + 2y = 7 or 3x + 2y – 7 = 0

6. On plotting the graphs of two lines, we find that their point of intersections is (2, 1/2) as shown in fig. 15.2.

Figure 15.2

7. The equations of the line passing through the point of the intersection (2, 1/2) of the two given line is :
(3x - 2y - 5) + λ (3x + 2y - 7) = 0 At λ= 1, -1, 2, 1/2 ………..(1)

8. Putting λ = 1 in equation (1), we get
(3x - 2y - 5) + 1 (3x + 2y - 7) = 0
⇒ 6x - 12 = 0
Putting x = 2 we get
6 x 2 – 12 = 0
0 = 0
Therefore for λ = 1 , equation (1) is satisfied by the point of intersection of the two given lines.

9. Putting λ, in equation(1) we get
(3x - 2y - 5) - 1 (3x + 2y - 7) = 0
3x - 2y - 5 - 3x - 2y + 7 = 0
- 4y + 2 = 0
Putting y = 1/2 in this equation, we get
-4 x 1/2 + 2 = 0
-2 + 2 = 0
0 = 0
Therefore for λ = 1 , equation(1) is satisfied by the point of intersection of the two given lines.

10. Proceeding as above, we can prove that for λ= 2 and 1/2 ,the equation(1) is satisfied by the point of intersection of the two given lines.

Observations

1. For λ = 3, the equation of the line passing through the point of intersection of the two given lines i.e. equation (1) becomes,
(3x - 2y - 5) + 3 (3x + 2y - 7) = 0
Or 3x - 2y – 5 + 9x + 6y – 21 = 0
Or 12x + 4y – 26 = 0
Putting x = 2, y = 1/2 , we get
12 x 2 + 4 x 1/2 - 26 = 0
24 + 2 – 26 = 0
26 - 26 = 0
Therefore, for λ = 3 equation (1) is satisfied by the point of intersection of the two given lines.

2. Similarly we can prove that equation (1) is satisfied by the point of intersection of the two given lines for λ = 4, 5, 6 ……. . It verifies that the equation of a line passing through the point of intersection of the equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 is of the form

a₁x + b₁y + c₁ = 0 + λ( a₂x + b₂y + c₂) = 0

Result

Equation of a line passing through the point of intersection of two lines a₁x + b₁y + c₁ = 0  and a₂x + b₂y + c₂ = 0  is of the form  a₁x + b₁y + c₁ = 0 + λ( a₂x + b₂y + c₂ = 0)

Applications

1. This activity can be used to understand the result relating to the equation of a line passing through the point of intersection of the two given lines.

2. This activity also leads to the conclusion that an infinitely many lines pass through a fixed point.

VIVA – VOICE

Q. 1. What is the general equation of a straight line?

Ans  The general equation of a straight line is ax + by + c = 0  Where a and b are not the zero simultaneously.

Q.2 what is a slope of line?

Ans.  Slope of a line is defined as the tangent of the angle, which the line make with the positive direction of x- axis.

Q.3 What is a condition that the two lines a₁x + b₁y + c₁ = 0  and a₂x + b₂y + c₂ = 0  where   

(i) parallel to each other ?

(ii) perpendicular to each other?

Ans  (i)   

         (ii)   

Q.4  How many lines can be drawn from the point of intersection of two given straight lines?

 Ans.  Infinitely many lines can be drawn

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW