Mathematics Lab Activity-3 Class XI

Mathematics Laboratory Activities on set theory for class XI students Non-Medical. These activities are strictly according to the CBSE syllabus

Chapter - 1 | Set Theory

Activity - 3

Objective

To verify distributive law for three non-empty sets A, B and C, that is 

A⋃ (B ⋂ C) = (A⋃B)⋂(A ⋃C)

Material Required

Hardboard, thick sheet of paper, pencil, colours, scissors, adhesive.

Theory

Distributive Law

For any three sets A, B and C, we have :

1. A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)

2. A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C)

Procedure

 1. Cut five rectangular strips from a sheet of paper and paste them on the hardboard so that three of the rectangles are in horizontal line and paste the remaining two rectangles also horizontally in a line just below the above three rectangles.

2. Write the symbol U in the left or right corner of each rectangle as shown in the figures below. U denotes the universal set represented by the rectangles.

3. Draw three circles and mark them as A, B, C in all the rectangles. Circles A, B, and C represent the subsets of the universal set U.

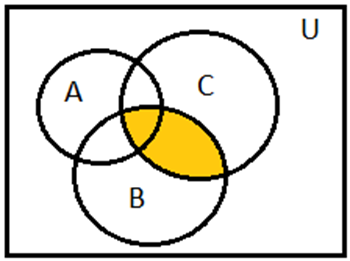
        Fig 4.1     B ⋂ C                             

Fig 4.2    A ⋃ B                  

Fig 4.3    A ⋃ C

 

Fig. 4.4   A ⋃ (B⋂C)                             Fig. 4.5   (A⋃B)⋂(A⋃C)

Observations

1. In figure 4.1 colored  portion represents B ⋂ C

2. In figure 4.2 colored  portion represents  A ⋃ B .

3. In figure 4.3 colored  portion represents A ⋂ C .

4. In figure 4.4 colored  portion represents A ⋃ (B ⋂ C) .

5. In figure 4.5 colored  portion represents A ⋃ B) ⋂ (A ⋃ C)

6. On measurement common colored portion in fig. 4.4  is equal to the colored portion in figure 4.5.    A ⋃ (B ⋂ C) = A ⋃ B) ⋂ (A ⋃ C)

Result

Distributive property is verified A ⋃ (B ⋂ C) = A ⋃ B) ⋂ (A ⋃ C)

Simlarly Distributive property A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C) can also be verified

Applications

The distributive law of set operations is used in the simplification of problems involving set operations.

VIVA – VOICE

Q. 1. What are the properties of the operations of union of two sets ?

Ans. Operations of union of two sets have the following properties :

i) It holds commutative law :  A ⋃ B = B ⋃ A       

ii) It holds Associative law   :   (A ⋃ B) ⋃ C  =  A ⋃ (B ⋃ C)

iii) Law of identity element: A ⋃ ɸ = ɸ ⋃ A = A

iv)  Idempotent Law : A ⋃ A = A

v) Law of universal set: U ⋃ A = U

Q. 2. What are the properties of the operation of intersection of two sets ?

Ans. The operation of intersection of two sets has the following properties :

i) It holds commutative law :   A ∩ B = B ∩ A

ii) It holds Associative law :     A ∩ (B ∩ C) = (A ∩ B) ∩ C 

iii) Law of identity element:     A ∩ ɸ = ɸ ∩ A = ɸ

vi) It holds the distributive law :   A ∩ (B ⋃ C) = (A ∩ B) ⋃ (A ∩ C) 

v) Law of Universal set:   U ∩ A = A

vi) Idempotent Law : A ∩ A = A

Q. 3 Which set theory is used in the present day mathematics?

Ans. Georg cantor’s set theory.

THANKS FOR YOUR VISIT
PLEASE COMMENT BELOW