Mathematics Lab Activity-17 Class X | Area Related to Circle

  Mathematics Lab Activity-17 Class X

Mathematics Laboratory Activities on Tangent to a Circle for class X students with complete observation tables strictly according to the CBSE syllabus.

Chapter - 11

area related to circle

Activity - 17

Objective

To obtain formula for area of a circle experimentally.

Material Required

Threads of different colours, scissors, cardboard, thick sheet of paper, adhesive, ruler.

Procedure

1. Draw a circle of radius say r units on a thick sheet of paper, cut it out and paste it on the cardboard.

2. Cut the coloured threads of different sizes in pairs.

3. Fill up the circle by pasting one set of coloured threads of different sizes in concentric pattern so that there is no gap left in between the threads as shown in Fig. 1.

Figure 1

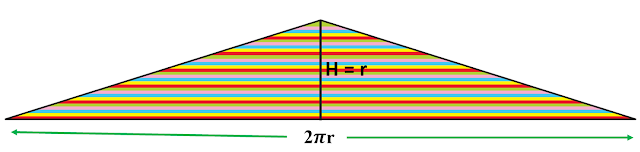
4. Arrange the other set of coloured threads starting from smallest to the largest in the pattern shown in Fig. 2. Last thread will be of same colour and same length as that of the outermost thread of the circle as shown in Fig. 2.

Figure 2

5. Number and size of threads pasted on the circle and number and size of thread pasted in the form of triangle are the same.

6. Therefore, area covered by threads on the circle and area of triangular shaped figure formed by threads is the same.

Observations & calculations

1. Area of triangle = (1/2) Base × Height.

2. Base of the triangle = Circumference of the circle (2πr) 

3. Height of the triangle = Radius of circle ( r).

4. Area of the circle = Area of triangle 

                                

                               

On actual measurement:

5. Base of the triangle = 12 cm units.

6. Height of triangle     = 7 cm units (i.e., radius of the circle).

7. Area of triangle         =  (1/2)×(Base × Height) sq. units.

8. Area of circle             = Area of triangle 

                                         = (1/2) × 12× 5

                                         = 30 cm².

Result

From this we conclude that in a circle radius is always perpendicular to the tangent at the point of contect.

Applications

This result can be used in finding areas of flflower beds of circular and semi-circular shapes and also for making circular designs and in estimating the number of circular tiles required to cover a floor.

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW