Lesson Plan, Class XI (Ch-2) | Relations & Functions

LESSON PLAN   SUBJECT MATHEMATICS

CLASS 10+1

lesson plan for maths class XI cbse,   Method to write lesson plan for maths class 11, lesson plan for maths class XI, lesson plan for maths teacher in B.Ed.

TEACHER  :   DINESH KUMAR	SCHOOL :  RMB DAV CENTENARY PUBLIC SCHOOL NAWANSHAHR
SUBJECT   :   MATHEMATICS	CLASS                  :   XI  STANDARD BOARD                 :  CBSE
LESSON TOPIC / TITLE   :  CHAPTER 2: Relations & Functions	ESTIMATED DURATION:  This lesson is divided into seven modules and it is completed in 10 class meetings.

PRE- REQUISITE KNOWLEDGE:-

Set theory chapter 1 class 11   math-lesson-plan-class-xi-chapter-1

TEACHING AIDS:- 

Green Board, Chalk,  Duster, Charts, smart board, projector, laptop etc.

METHODOLOGY:-   Lecture method  and Demonstration

OBJECTIVES:-

• Ordered pair, Cartesian product of sets. Number of elements in the Cartesian product of two sets.

• Cartesian product of the sets of reals with itself (up to R x R x R )

• Definition of relation, pictorial diagrams, domain, co-domain and range of a relation.

• Function as a special type of relation, pictorial representation of a function, domain, co-domain and range of a function.

• Real valued functions, their domain and range.

• Constant, identity, polynomial, rational, modulus, signum, exponential, logarithmic and greatest integer functions with their graphs.

• Sum, difference, product and quotient of functions.

LEARNING OUTCOMES

 After studying this lesson, students will be able to explain the 

• Cartesian product of two sets.

• Numbers of subsets and number of relations from cartesian product.

• Domain, Range and Codomain of relations.

• Definition of function and types of functions.

• Domain and range of different types of functions.

• Operations on functions.

RESOURCES

NCERT Text book of Mathematics

NCERT Exemplar Text Book

RESOURCE CENTRE at cbsemathematics.com

DAV Resource Material for class 10

KEY WORDS :
Relations, Functions, Domain, Range, Codomain, Cartesian Product, Modulus functions, Logarithmic functions, Signum functions, Greatest Integer functions

(CONTENT & PRESENTATION)

• Cartesian Product of two sets.

• Number of relations from cartesian product.

• Domain, range and codomain of relations.

• Definition of functions.

• Domain and range of functions.

• Different types of functions.

LEARNING ACTIVITIES:

INTRODUCTORY ACTIVITY : Click Here

EXPERIENTIAL ACTIVITY : Click Here

ART INTEGRATED ACTIVITY : Click Here

PROCEDURE :-

Start the session by asking simple questions of set theory and their method of representations.  Now introduce the concept of relation and functions step by step as follows.  

PRESENTATION OF THE TOPIC 

[CLICK HERE FOR COMPLETE  EXPLANATION]

Cartesian Product of two sets

If A and B are two sets then Cartesian product A X B is the set of all ordered pairs of elements from A to B, i.e.

          A X B = { (a, b) : a ∈ A, b∈ B }

First element of all the ordered pair  belongs to set A and second element belongs to set B.

If either A or B is a null set, then A X B will also be  empty set. In this case we can write A X B = φ

Ordered pair of elements:

An ordered pair of elements taken from two sets A and B is a pair of elements written in small brackets and grouped together in a particular order. i.e. (a, b).

Equal Ordered Pairs : 

Two ordered pairs are equal if and only if the corresponding first elements are equal and the second elements are also equal.

In general : 

Note:

i) If there are p elements in set A and q elements in set B, then there will be  pq elements in A X B.

 i.e. if n(A) = p and n(B) = q, then n(A x B) = pq.

ii) If A and B are non zero sets and either A or B  is an infinite set, then A X B is also an infinite set.

iii) A X A X A  = {(a, b, c) : a, b, c ∈ A }

Example :

Let A = {1, 2} and B = {3, 5, 8}, then

A X B = {1, 2} X {3, 5, 8}

          = {(1, 3), (1, 5), (1, 8), (2, 3), (2, 5), (2, 8)}

Here n(A) = 2, n(B) = 3,  n(A X B) = 6 = 2 x 3

⇒ n(A x B) = n(A) x n(B)

Relations

A relation R from set A to set B is the subset of Cartesian product A x B.

In Cartesian product A x B, number of relations equal to the number of subsets.

Domain

Set of all first elements of the ordered pairs in the relation R is called its domain.

Range

Set of all second elements of the ordered pairs in the relation R is called its range.

In any ordered pair second element is also called the image of first element.

Co-domain of the relation: 

The whole set B is called the co-domain of the relation R.

Example
In the above figure 
A X B = {(a₁, b₁), (a₁, b₂), (a₁, b₃), (a₂, b₁), (a₂, b₂), (a₂, b₃) }

Domain = {a₁, a₂ }

Range = { b₁, b₂, b₃}
n(A) = 2, n(B) = 3,  n(A X B) = 2 x 3 = 6
Number of subsets of A x B = 2⁶ = 64   
Number of relations of A X B = 2⁶ = 64   

Function their Domain, Range & Co-domain

Function

A relation is said to be a function If no two ordered pairs have same first element. A function from A to B is denoted by f : A→B

In a relation if different elements of set A has different images in set B then the relation is called a function

Example(1) :

f(x) = {(1, 2), (2, 3), (3, 4), (4, 5), (10, 20)}

Image of 1 = 2      ⇒ f(1) = 2

Image of 2 = 3      ⇒ f(2) = 3

Image of 3 = 4      ⇒ f(3) = 4

Image of 4 = 5      ⇒ f(4) = 5

Image of 10 = 20  ⇒ f(10) = 20

So different elements have different images, hence it is a function.

Example (2) :

f(x) = {(1, 2), (2, 3), (2, 4), (4, 5), (10, 20)}

Image of 1 = 2      ⇒ f(1) = 2

Image of 2 = 3      ⇒ f(2) = 3

Image of 2 = 4      ⇒ f(2) = 4

Image of 4 = 5      ⇒ f(4) = 5

Image of 10 = 20

Here we see that element 2 has two images 3 and 4, so it is not a function.

Domain of a function f : A→B

All those elements of set A which have their image in set B is called domain of a function.

Range of a function f : A→B

Set of all those elements of set B which have their pre-image in set A is called range of function.

Co-domain of a function f : A→B

Whole set B is called the co-domain

Real function and Real valued function: 

A function whose domain is either R or a subset of R then it is called a real  function. A function whose range is either R or a subset of R then it is called a real valued function.

Some Functions And Their Graphs

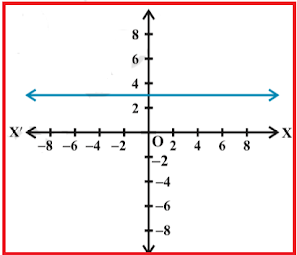
Constant Function :

A function f : R→ R defined by f(x) = c, where c is a constant is called a constant function

Domain = R or (-∞, ∞)

Range = {c} or [c, c]

For the constant function f(x) = c, the domain consists of all real numbers; there is no restrictions on the input. The only output value is the constant c, so the range is the set {c} that contains this single element. In interval notation, this is written as [c, c]. 

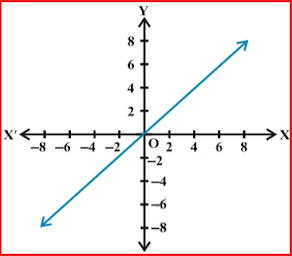
 Identity Function :

A function f : R→ R defined by f(x) = x is called an Identity function

Domain = R or (-∞, ∞)

Range = R or (-∞, ∞)

For the identity function f(x) = x, there is no restriction on x. Both domain and range are the set of all real numbers.

Modulus Function :

A function f : R→ R defined by  f(x) = |x| is called a modulus function.

Domain = R or (-∞, ∞)  and  Range = Positive Real Numbers including '0' or [0, ∞)

For the absolute value function f(x)=|x|, there is no restriction on x (domain). However, because absolute value is defined as a distance from 0, the output (range) can only be greater than or equal to 0.

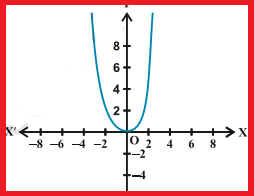
Quadratic polynomial  Function :

A function f : R → R defined by  f(x) = x²  is called a quadratic polynomial function.

Domain = R or (-∞, ∞)   

Range = Positive real numbers or  (0, ∞)

For the quadratic function f(x) = x², the domain is all real numbers because the horizontal extent of the graph is the whole real number line. Since the graph does not include any negative values for the range, the range is only non-negative real numbers.

Cubic Polynomial  Function :

A function f : R→ R defined by  f(x) = x³  is called a Cubic Polynomial Function

Domain = R or (-∞, ∞) and  Range = R or (-∞, ∞)

For the cubic function f(x) = x³, the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.

Reciprocal Function

A function defined by f(x) =    is called a reciprocal function

Domain = (-∞, 0) ⋃ (0, ∞) or  R - {0}

Range = (-∞, 0) ⋃ (0, ∞) or R - {0}

For the reciprocal function f(x)=  , we cannot divide any number by 0, so we must exclude 0 from the domain. Further, 1 divided by any value can never be 0, so the range also will not include 0. 

Reciprocal Squared Function

A function of the type f(x) =    is called a Reciprocal Squared Function.

Domain = (-∞, 0) ⋃ (0, ∞) or  R - {0}

Range = (0, ∞) or  Positive Real Numbers

For the reciprocal squared function f(x) =  , we cannot divide by 0, so we must exclude 0 from the domain. There is also no x that can give an output of 0, so 0 is also excluded from the range as well. Note that the output (Range) of this function is always positive due to the square in the denominator, so the range includes only positive Real numbers.

Square Root Function:

A function f(x) =  is called a square root function

Domain = [0, ∞)

Range = [0, ∞)

For the square root function f(x)= , we cannot take the square root of a negative real number, so the domain must be 0 or greater than "0". The range also excludes negative numbers because the square root of a positive number x is defined to be positive square root of negative number is negative.

Cube Root Functions

A function f(x) =   is called a cube root function.

Domain = R or (-∞, ∞)

Range =  R or (-∞, ∞)

For the cube root of a function f(x) =  , the domain and range include all real numbers. Note that cube root of positive number is positive and cube root of negative number is negative.

Signum Function :

The function f : R → R defined by 

 is called a signum function.

Domain of signum function is the set of real numbers.

Range of signum function is = {-1, 0, 1}

Graph of signum function is given below

Greatest Integer Function

The function f: R→ R defined by f(x) = [x], where x ∈ R, assumes the value of the greatest integer, less than or equal to x. This function is called the greatest integer function.

Domain of Greatest integer function is All real numbers.

Range of Greatest integer function = Set of all integers.

For examples [1.1] = 1,  [1.5] = 1,  [1.9] = 1

[5.3] = 5,   [5.8] = 5,  [-7.3]=-8,  [-7.9] = -8 

Undefined Terms : 

The terms like    are called the undefined terms. This situation is not valid for finding the limit of a function.

STUDENTS DELIVERABLES:-

• Review questions given by the teacher.  
• Students can make a pictorial representation showing relation and functions with their domain, co-domain and range. 
• Solve NCERT problems with examples and some extra questions from refreshers.

EXTENDED LEARNING:-

Students can extend their learning in   through the Resource Centre Mathematics . Students can also find many interesting topics on mathematics at the site:   cbsemathematics.com

ASSESSMENT TECHNIQUES:-

Assignment sheet will be given as home work at the end of the topic. Separate sheets which will include questions of logical thinking and Higher order thinking skills will be given to the above average students.

Class Test , Oral Test , worksheet and Assignments. can be made the part of assessment.

Re-test(s) will be conducted on the basis of the performance of the students in the test.

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW